
この記事では、トレンドの方向が分かるテクニカル分析を紹介していきます。
トレンドの方向がわかれば株式投資やFXで利益を上げられるようになります。
トレンドとは、相場が動いていくやや長めの方向をいいます。
相場は、細かい上下を繰り返しながら、しばらく一定方向に進む特徴があります。
この流れを把握して、それに乗っていくための分析をトレンド分析といいます。
合わせて読みたい記事
単純移動平均(SMA:Simple Moving Average)
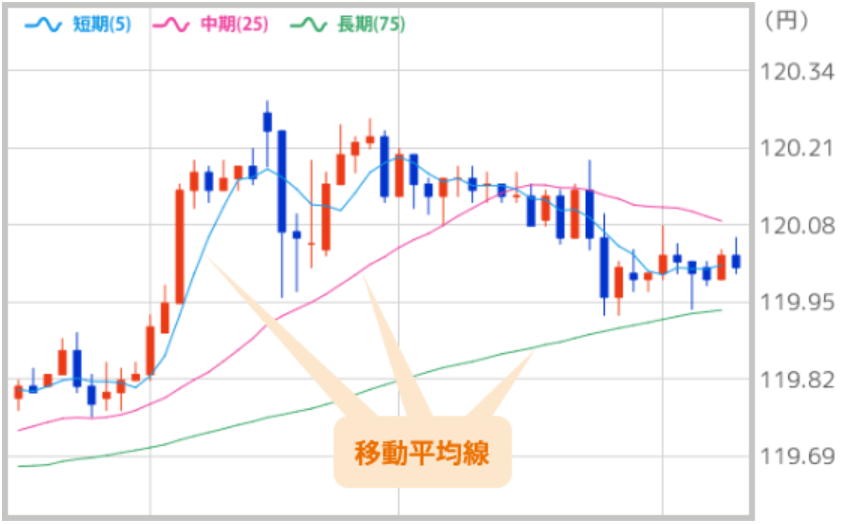
出典:auじぶん銀行
変化が激しい価格推移の中から趨勢的な傾向を知るため、近似する直線(トレンドライン)を引くことがあります。
しかし、これは線を引く人によって線の位置が微妙にずれ、判断も変わるので難儀です。
そこで考案されたのが移動平均(MA)です。
1901年にアーサー・ボーレイが書いた『統計学の基礎(Elements of Statistics)』には、いろいろな移動平均が紹介されています。
移動平均は、価格を平均して繋げただけですが、これにより、計算期間の中で一時的に生じた高値や安値は均されてしまい、本質的な変化の傾向、すなわちトレンドが抽出されます。
しかも、計算に用いる価格や計算期間が同じなら、誰が計算しても同じ値になります。
したがって、移動平均は、手で引くトレンドラインに比べて、使い手の主観が入りにくいトレンドラインだということができます。
価格推移の基調は、移動平均が右上がりなら上昇トレンド、右下がりなら下降トレンドです。
移動平均の傾きが急角度なら相場の勢いは強く、水平に近づくほど勢いは弱いことになります。
計算の仕方
あらかじめ決められた期間の終値を合計し、終値の数で割ります。
他と区別するため、単純移動平均(SMA)と呼ばれることもあります。
日足では1週間相当の5日、1ヵ月相当の20日や25日などがよく使われています。
週足では四半期相当の13週間、半年相当の26週、1年相当の52週。
月足では1年の12ヵ月、2年の24ヵ月、5年の60ヵ月などが使われます。
平均すると、計算期間内のデコボコは打ち消され、計算期間より長い変動だけが残されます。
したがって、短期的な傾向を知りたければ計算期間を短くし、長期的な傾向を知りたければ長くします。
さらに、短期移動平均から長期移動平均を差し引くと、短期移動平均の計算期間よりも長く、長期移動平均の計算期間よりも短い、中間の周期を持つ変動だけを取り出すこともできます。
自分の投資期間に合った計算期間を選択するのがよいでしょう。
移動平均と株価の関係でトレンドが分かる
上昇トレンドにあるときは、価格は移動平均より上で推移し、滅多に移動平均を下回りません。
反対に、下降トレンドにあるときは、価格は移動平均より下で推移し、滅多に移動平均を上回りません。
この関係は、計算期間の短い短期移動平均と、長い長期移動平均でも同様です。
上昇トレンドでは短期移動平均は長期移動平均の上で推移し、滅多に長期移動平均を下回りません。
下降トレンドでは、短期移動平均は長期移動平均の下で推移し、滅多に長期移動平均を上回りません。
したがって、価格と長短移動平均の位置関係をみるとトレンドの方向が分かります。
また、上昇傾向が安定しているときには、上から順番に価格、短期移動平均、長期移動平均の順になります。
反対に下落傾向が安定しているときには、下から順に価格、短期移動平均、長期移動平均となります。
この順番が乱れているときは、トレンドの基調が変化する可能性があります。
ゴールデンクロス(GC)とデッドクロス(DC)
トレンドが上昇から下落に転じる場面では、価格が下落に転じて短期移動平均、長期移動平均の順に割り込み、次に短期移動平均が下落に転じて長期移動平均を割り込み、最後に長期移動平均が下落に転じます。
反対に、トレンドが下落から上昇に転じる場面では、価格が上昇に転じて短期移動平均、長期移動平均の順に上回り、次に短期移動平均が上昇に転じて長期移動平均を上回り、最後に長期移動平均が上昇に転じます。
このとき、短期移動平均が長期移動平均を上回る場面をゴールデンクロス(GC)、短期移動平均が長期移動平均を下回る場面をデッドクロス(DC)と呼びます。
大勢が方向転換する場合には、必ずゴールデンクロスやデッドクロスが起こりますが、ゴールデンクロスやデッドクロスとなっても必ず大勢が方向転換するとは限りません。
ゴールデンクロスは上昇転換を示唆するので買いシグナル、デッドクロスは反対に売りシグナルとされますが、移動平均の計算期間を数週間以上と長めにする方が成功率が高いようです。
指数平滑移動平均(EMA:Exponential Moving Average)
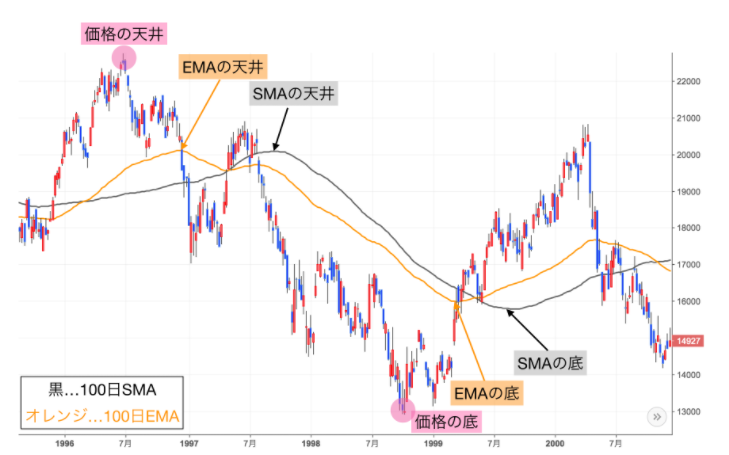
出典:小次郎講師のチャート情報局
価格が直線的に上昇または下降している場面を想定すると、移動平均は常に計算期間の中央にある値と一致します。
このことから、単純移動平均には基本的に計算期間の半分だけ遅れる性質があることが分かります。
当然、ゴールデンクロスやデッドクロスなどのシグナルも実際の相場より遅行します。
この遅行は、計算期間が短ければ無視できますが、長い場合には致命的になる可能性があります。
指数平滑移動平均(EMA)はその遅行性を改善したもので、単純移動平均と同じくらいよく用いられています。
移動回帰値(LRI:Linear Regression Indicator)
価格推移に傾向線を引くとき、すべての価格からの距離の合計が最も少なくなる位置に引くという方法があります。
この計算方法を最小二乗法といい、遺伝の研究から生まれました。
引かれた線を回帰直線といいます。
回帰直線を引くと、価値はその線を中心として上下しているように見えます。
この線の右端の値を連続させたものが移動回帰値(LRI)で、エンドポイント移動平均(EPMA:End Point MA)ともいいます。
Excelで計算するにはSLOPE関数とINTERCEPT関数を使う方法もありますが、FORECAST関数を使う方が簡単でしょう。
MACD(Moving Average Convergence,Divergence:移動平均収束発散法)
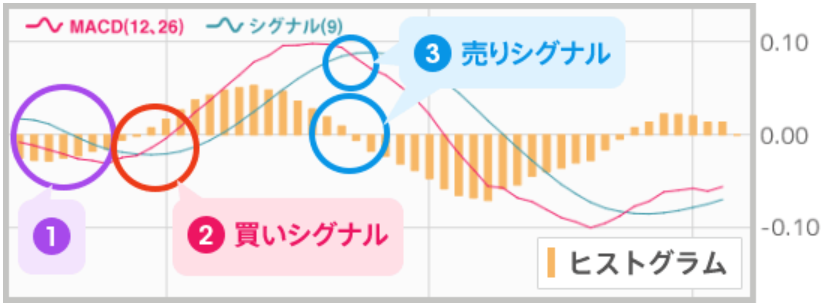
出典:auじぶん銀行
MACDは「マックディー」と読みます。
「移動平均収束発散法」という名称もありますが、MACDの方が一般的でしょう。
1979年に米国のジェラルド・アペルが考案した方法で、古い手法ですが、重要な発想が含まれています。
MACDは短期移動平均から中期移動平均を引いたものです。
移動平均には計算期間よりも短い周期を持つ変動だけを打ち消すという性質があります。
これは、裏を返すと、計算期間よりも長い周期を持つ変動だけを残していることになります。
つまり、短期移動平均には、短期・中期・長期の周期を持つ変動が含まれています。
したがって、その差であるMACDには、短期の価格変動だけが残されていることになります。
以上から、MACDがプラスの値のときには、価格が短期的な上昇トレンドにあり、値が大きいほど、上昇の勢いは強いといえます。
反対に、MACDがマイナスのときには、価格は短期的な下降トレンドにあり、値が小さいほど、下落の勢いは強いといえます。
同時に、MACDがマイナスからプラスに転じるときは、トレンドが下落から上昇に転じる場面、MACDがプラスからマイナスに転じるときは、トレンドが上昇から下落に転じる場面といえます。
計算の仕方
ジェラルド・アペルは、単純移動平均で計算してもよいとしていますが、普通は指数平滑移動平均を用いて計算します。
$$MACD=終値の12日EMA-終値の26日EMA$$
$$シグナル=MACDの9日EMA$$
$$ヒストグラム=MACD-シグナル$$
当日の指数平滑移動平均(EMA)=前日のEMA+α×(当日の値-前日のEMA)
α=2÷(n+1)
n:計算期間(12、26、9)
EMAの初期値:値のn日単純平均
値:MACDを計算するときは終値、シグナルを計算するときはMACD
シグナルとヒストグラム
MACDはトレンドの方向を表していますが、その平均であるシグナルは、トレンドの平均的な方向と強さを表していることになります。
では、MACDからシグナルを差し引いたヒストグラムは、何を表しているのでしょうか?
MACDで使うヒストグラムは、統計で使う度数分布図とは関係がありません。
考案者がMACDとシグナルは折れ線グラフ、ヒストグラムは棒グラフで描いていたことによるものかもしれません。
ヒストグラムは、足元のトレンドがトレンドの平均値よりも強いか弱いかを表しています。
つまり、MACDがプラスのときに、ヒストグラムがプラスなら上昇ペースが加速しており、ヒストグラムがマイナスなら上昇ペースが減速していることを意味します。
反対に、MACDがマイナスのときに、ヒストグラムがマイナスなら下降ペースが加速しており、ヒストグラムがプラスなら下降ペースが減速していることになります。
しかし、実際の価格推移とMACD、シグナル、ヒストグラムの推移を注意深く見くらべてみると、価格推移の天井や底と、MACDやシグナルの天井や底とはあまり一致していません。
むしろ、価格推移の天井はヒストグラムがプラスからマイナスに転じる場面、価格推移の底はヒストグラムがマイナスからプラスに転じる場面と近いことも多いようです。
使い方は、理屈ではなく実際に即した工夫が必要なようです。
